--

深度学习 01： miniflow

本文代码下载
Tensorflow 利用一个计算图（computer graph）把从输入到输出统合到一起，利用你定义的模型（比如linear regression 线性回归、logisticre gression 洛吉斯蒂回归或者 convolutional neural network 卷积神经网络等等，当中有很多的模型的参数，参数的值待定，一开始一般为随机值），从输入计算出一个预测的输出，再用你的预测输出与真实结果进行比较，计算出一个损失函数（Loss Function）。

在数学上，我们可以用一个非常复杂的表达式直接写出从输入到输出以及从输入到损失函数的关系，从这个表达式中可以计算出损失函数对于模型中间参数的导数。

我们的目标是找出最好的模型，也就是找到那些模型参数，使得对于我们的输入的损失函数有最小值，这样我们的模型对于输入额预测也就最准。

利用梯度下降的方法（gradient descent），我们每次按照梯度下降的方向改变这些模型参数，直到梯度降低为 0（或者小于一定的阈值），模型收敛。

利用这个训练出来的模型，我们就可以对于新的输入进行预测了。

在实际每个参数的梯度计算中，我们利用的是链式法则，从后往前（也就是从损失函数到输入），逐步计算每一层节点的梯度。这个过程被称之为反向传播（back propagation）。

而从输入到输出的从前往后的计算过程，我们称之为前向传播（forward pass）。

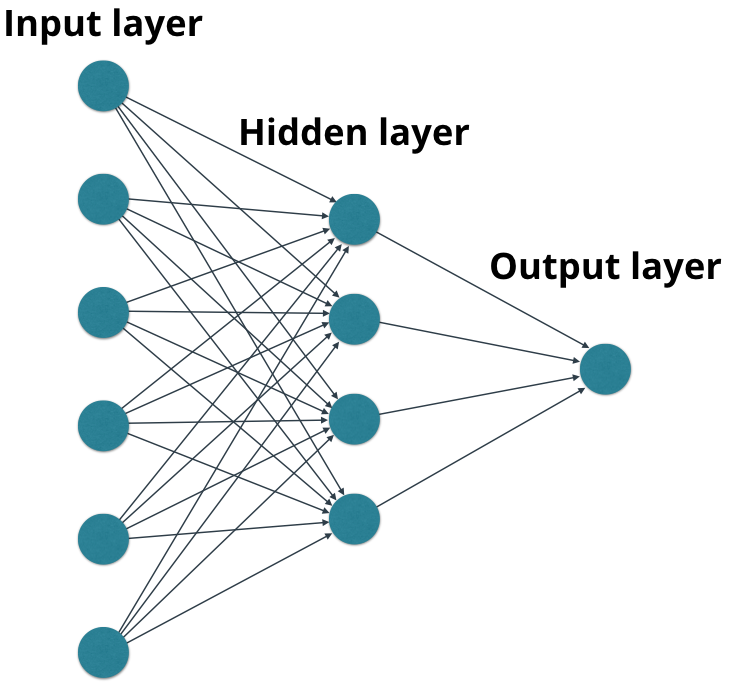
由于 tensorflow 的代码结构非常复杂，为了厘清上述概念，我们利用 miniflow 来实现并分析每个节点是如何进行前向传播和反向传播的（forward pass，back propagation），同时他们是如何整合成一个计算图来完成整个模型的训练的。

这里有一份很简单的miniflow 代码，可以在我的 github 找到， https://github.com/easyfly007/miniflow/

更为详细的实现可以参考这里： http://neuralnetworksanddeeplearning.com/

import numpy as np

class Node(object):
	def __init__(self, inbound_nodes = []):
		self.inbound_nodes = inbound_nodes
		self.outbound_nodes = []
		for n in self.inbound_nodes:
			n.outbound_nodes.append(self)
		self.value = None
		self.gradients = {}
	
	def forward(self):
		raise NotImplementedError

	def backward(self):
		raise NotImplementedError

这是一个有待继承的 Node 基类，它提供了构造函数，以及两个接口定义 forward 和 backward。 Node 是什么？这里的物理含义是神经网络的一层 layer。（是不是命名为 Layer 更好一些？）

这个 Node 的类它有：
inbound_nodes 为输入层的节点列表，outbound_nodes 为该层输出的节点列表，以及该层的输出的节点的值列表 value 和节点值的 gradients 梯度，当然它应该还有和 Node 类型相关的参数，这个应不同的实现而异，有待于在继承的具体 Node 中来定义。

下面我们来定义一个输入 Node:

	
class Input(Node):
	def __init__(self):
		Node.__init__(self)

	def forward(self, value = None):
		if value is not None:
			self.value = value

输入节点的 forward pass 很简单，就是更新一下 value 而已。

下面我们来定义一个叫做 Add 的 Node，他可以把输入节点的值求和。

class Add(Node):
	def __init__(self, x_list):
		Node.__init__(self, x_list)

	def forward(self):
		self.value = 0.0
		for node in self.inbound_nodes:
			self.value += node.value

可以看到，通过一次 forward，Add 这个 Node 的值更新为的他的输入的 inout 节点的值的和。

下面我们来定义一个叫做 Linear 的 Node，来实现 Y = W * X + B 的线性组合计算，其中有三个输入节点 W，X，B：

w 是 [n2, n1] 的系数矩阵，
x 是 [n1, ] 的输入节点向量，
b 是 [n2, ] 的偏置系数
y 是 [n2, ] 的输出节点向量


class Linear(Node):
	def __init__(self, [inputs, weights, bias]):
		Node.__init__(self, [inputs, weights, bias])

	def forward(self):
		x = np.array(self.inbound_nodes[0].value)
		w = np.array(self.inbound_nodes[1].value)
		b = np.array(self.inbound_nodes[2].value)
		self.value = np.dot(w, x) + b

有了以上的几个，我们可以写出一个最简单的线性回归计算图的 forwrad pass 了。

我们来定义一个 fowward pass 的函数，

def forward_pass(output_node, sorted_nodes):
	'''
	perform a forward pass through a list of sorted nodes
	arguments:
		output_node: the output node of the graph (no outgoing edges)
		sorted_nodes: a topologically sorted list of nodes
	returns the output node's value
	'''
	for n in sorted_nodes:
		n.forward()

	return output_node.value

这里 sorted_nodes 包含了一个完整的从输入到输出的有序排列的 node 列表。

我们一开始定义了各种 node，以及他们的前后连接关系（指的是Node A 是 Node B的输入节点，而Node B 又是Node C 的输入节点等等），而这个就是一个计算图的结构。

有了 linear Node，我们可以做 regression 的预测，而对于 classification 或者多层的 linear，我们需要定义至少一种的非线性激活函数，比如 sigmoid 现在就来写一个：

class Sigmoid(Node):
	def __init__(self, x):
		Node.__init__(self, [x])

	def _sigmoid(self, x):
		return 1.0/(1.0+ np.exp(-x))
	
	def forward(self):
		x = self.inbound_nodes[0].value
		self.value = self._sigmoid(x)

以上，我们就可以来做一个 forward pass 了，从一个输入利用 logistic regresison 做出一个预测。也就是 Y_label = sigmoid(W*X + B)

	
def forward_pass(output_node, sorted_nodes):
    """
    Performs a forward pass through a list of sorted nodes.

    Arguments:

        `output_node`: A node in the graph, should be the output node (have no outgoing edges).
        `sorted_nodes`: A topologically sorted list of nodes.

    Returns the output Node's value
    """

    for n in sorted_nodes:
        n.forward()

    return output_node.value

当然我们提供一个从输入节点产生的整个 computer graph 的方法这里给一点解释： feed_dict 是我们的输入 Node，我么嗯要从这些给定的输入 Node 开始，按照 forward pass 的顺序，得到整个的 computer graph。如何确定这个顺序？从数学上说，一个 conputer graph 相当于一个有向无环图（DAG，Directed Acyclic Graph）。

1. 从 feed_dict 的输入 Nodes 开始，我们初始化一个nodes 的列表，我们要从feed_dict 开始推导出所有的后续Nodes 并产生一个 Graph。
2. 我们不断从 nodes 列表中 pop 出一个 Node，来看它的输出节点，并把输出节点加入到 nodes 列表中去。不断循环，直到我们把整个从 feed_dict 开始的所有后续 Nodes 遍历完毕。 2. 在这个过程中我们用一个 dict G 来记录下这个后续的 computer graph （也就是这些在 nodes 列表中出现过的 Node）。以及他们的互相输入输出依赖关系。
3. 继续从输入Nodes 开始，我们给输入Node 赋值，同时查看后续的节点，是不是输入完备的，也就是说，他们的输入节点都是可以从我们的 feed_dict 计算出来的。这样我们得到了一个所有可以用来计算的完整的 Graph 了。

def topological_sort(feed_dict):
    """
    Sort the nodes in topological order using Kahn's Algorithm.

    `feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node.

    Returns a list of sorted nodes.
    """

    input_nodes = [n for n in feed_dict.keys()]

    G = {}
    nodes = [n for n in input_nodes]
    while len(nodes) > 0:
        n = nodes.pop(0)
        if n not in G:
            G[n] = {'in': set(), 'out': set()}
        for m in n.outbound_nodes:
            if m not in G:
                G[m] = {'in': set(), 'out': set()}
            G[n]['out'].add(m)
            G[m]['in'].add(n)
            nodes.append(m)

    L = []
    S = set(input_nodes)
    while len(S) > 0:
        n = S.pop()

        if isinstance(n, Input):
            n.value = feed_dict[n]

        L.append(n)
        for m in n.outbound_nodes:
            G[n]['out'].remove(m)
            G[m]['in'].remove(n)
            # if no other incoming edges add to S
            if len(G[m]['in']) == 0:
                S.add(m)
    return L

现在，我们来简单的测试一下，这个 forward pass 是否能够正常工作：

x, y, z = Input(), Input(), Input()

f = Add((x, y, z))

feed_dict = {x: 4, y: 5, z: 10}

graph = topological_sort(feed_dict)
output = forward_pass(f, graph)

# should output 19
print("{} + {} + {} = {} (according to miniflow)".format(feed_dict[x], feed_dict[y], feed_dict[z], output))

Posted on 2018-08-21 by Yifei