--
决策树
sklearn 中的 decision tree
决策树算法是最简单的一种分类算法,如果用 sklearn 来做的话,两三行代码就可以实现。
sklearn decision tree github decision tree
from sklearn import tree X = [[0, 0], [1, 1]] Y = [0, 1] clf = tree.DecisionTreeClassifier() clf = clf.fit(X, Y) result = clf.predict([[2., 2.]]) print(result) result_prob = clf.predict_proba([[2., 2.]]) print(result_prob)
用另外一个数据集来试一下吧
from sklearn.datasets import load_iris
from sklearn import tree
iris = load_iris()
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)
import graphviz
dot_data = tree.export_graphviz(clf, out_file=None)
graph = graphviz.Source(dot_data)
graph.render("iris")
predict = clf.predict(iris.data[:1, :])
print(predict)
predict_prob = clf.predict_proba(iris.data[:1, :])
print(predict_prob)
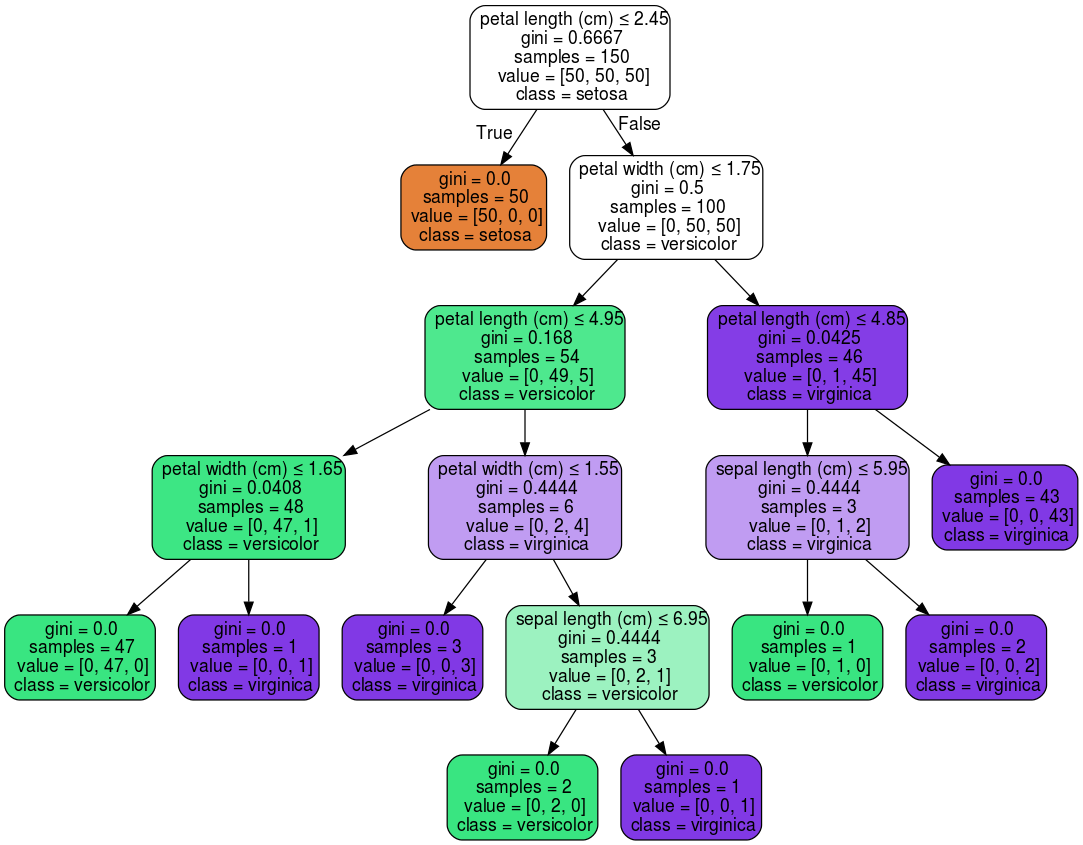
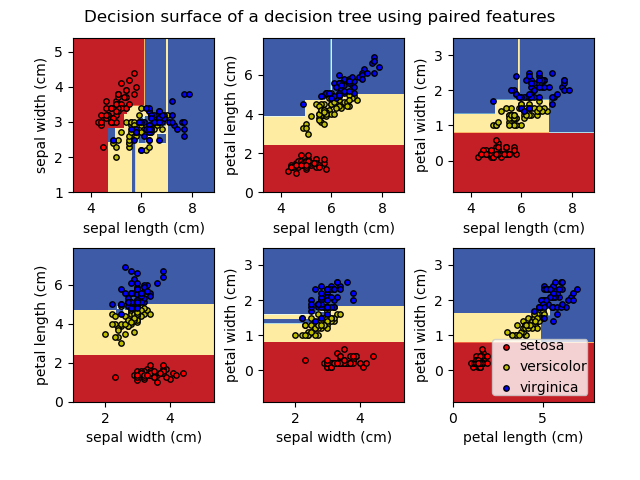
再回过头来看一下 sklearn 的 decision tree classifier 接口 decision tree classifier
以上我们简单的用 sklearn 调用来分类,我们具体来看一下里背后的算法原理。
以下内容来自 《统计学习方法》 (李航)第五章 -- 决策树
二分类的决策树
决策树就是在不断选取一个特征空间的一个特征,设定一个阈值,进行 if-else 的划分。
这种划分是互斥和完备的。也就是说,每一个样本,按照这种方式进行划分,能被而且只被一条划分的路径涵盖。
以 iris 数据集为例,有 4 个 feature,分贝是 sepal length,sepal width, petal width, petal length
同时有 3 个分类,Iris-Setosa, Iris-Versicolour, Iris-Virginica
首先选取一个 feature(feature A),在上面设定一个阈值 threshold A(ta),进行两分,小于 ta 的分为一组,大于 ta 的分为另外一组。
再对这两组样本继续在 feature B 上进行分类。
这个过程不断进行,直到样本被完全分好类或者没有 feature 可以供我们进行划分为止。
特征选取
如何选取特征? 我们用信息增益来衡量每个特征。
先定义什么叫做熵(entropy)。
在信息论中,熵表示随机变量不确定性的度量。
比如我们有一堆样本,每个样本的标签可以为 a 也可以为 b。
如果这些样本都为 a 标签,那么不确定性最低,熵最小。
如果这些样本处于完全的随机分布,也就是说,一半为 a,一半为 b,那么不确定性最大。
如果这些样本有 m 个为 a,n 个为 b,m > n,那么这个不确定性为以上两者之间。
我们给出一个数学上的定义,假设 X 是一个取有限值的离散随机变量,其概率分布为:
P(X= x_i) = p_i, i = 1, 2, 3, ..., n
H(X) = - SUM_i(p_i * log(p_i))
我们这里给定 log(0.) = 0.0
这里也可以记为
H(p) = - SUM_i(p_i * log(p_i))
那么我们定义信息增益为: 特征 A 对训练集 D 的信息增益 g(D, A), 为 集合 D 的经验熵 H(D) 于 特征 A 给定条件下 D 的经验条件熵 H(D|A) 的差。 也就是:
g(D, A) = H(D) - H(D | A)
这里所谓的经验的,是因为,我们无法知道实际的真实的分布,我们只能从采样的这些有限的样本中进行估计(特别是极大似然估计)来获得这个分布。(换句话说,我们要是知道实际的真实的分布,根本不用做这个分类器了,直接从该分布得出每种分类的概率即可)。
根据信息增益准则,我们按照如下规则选取特征:
对训练集(或者其子集) D, 计算其每个特征的信息增益,并比较他们的大小,选择信息增益最大的特征。
具体做法如下:
设 训练集为 D,大小为 m,有 k 个分类 C_k,k 为 1, 2, 3, ... K,
设 特征 A 有 n 个不同的取值,a_1, a_2, ..., a_n
计算信息增益如下:
1. 数据集 D 的经验熵:
H(D) = - SUM_k( |Ck| / |D| * log(|Ck| / |Dk|))
2. 特征 A 对数据集 D 的经验条件熵 H(D|A):
H(D|A) = SUM_n( |D_n| / |D|) * H(D_n)
D(D_n) = - SUM_k( |D_nk| / |D| * log2(|D_nk| / |D_n|))
g(D, A) = H(D) - H(D|A)
以上的根据信息增益最大来选取特征的做法,往往倾向于选择值较多的特征的问题。 我们可以用信息增益比(information gain ration)来进行校正。
信息增益比的定义如下:
gr(D,A) = g(D,A) / Ha(D)
Ha(D) = - SUM_n ( |Dn| / |D| * log(|Dn|/ |D|) )
决策树的生成
ID3 算法在决策树的各个结点利用信息增益准则选取特征,递归构建决策树。
具体做法如下:
1. 输入为数据集 D,特征 A, 阈值 e
2. 如果 D 中所有实例属于同一类 C_k, 则 T 为单结点树,返回 T
3. 如果 A 为空,则T 为单结点树,返回 T
4. 如果不是 2/3 中的情况,则对 A 中的每一个特征计算信息增益,选取最大的 Ag
5. 如果 Ag 小于阈值 e,则 T 为单结点树,以数据集 D 中数目最多的一类为类的标记,返回 T
6. 如果 Ag 大于阈值 e,对于 Ag 特征的每一个可选项,分割成若干子集,每一个子集重复1-> 6 的步骤
C4.5 算法
C4.5 相比于 ID3 算法, 利用信息增益比来选择特征。 步骤同上。
树的剪枝 prunning
ID3 和 C4.5 只有树的生成,容易过拟合。所以在生成了整颗决策树之后,需要进行剪枝处理来防止过拟合。
剪枝的过程就是降低树的复杂度。
我们需要重新定义 loss function。
我们定义决策树的损失函数为:
loss function, Ca(T) = SUM_t(Nt*Ht(T)) + a * |T|
Ht(T) = - SUM_k(N_tk / Nt * log(Ntk/Nt))
其实也就是增加了一个对于树的复杂度的惩罚项,|T| 表示树的复杂度。
可以用动态规划来递归的计算 |T|,方法如下:
1. 生成整颗决策树 以及参数 a
2. 计算每个结点的经验熵
3. 递归的从每个节点开始向上回缩
比较回缩之前和之后的损失函数,如果回缩之后的损失函数比较小,那么采用回缩进行剪枝,否则保持不变
4. 重复 3,直到无法进行回缩为止。
CART 算法
决策树不仅可以用来做分类,也可以用来做回归。前者叫做分类树,后者叫做回归树。
CART 是 classification and regression tree 的简称,分类与回归树。
对于回归树利用平方误差最小准则,
对于分类树利用基尼系数最小化准则。
对于回归树,我们选定一个 feature,然后用一个阈值 t 进行两分,
对分到两边的两组样本计算各自的平均值,对每个样本针对该平均值计算平方误差,求出使得平方误差最小的 t。
我们对每个 feature 都计算最小平方误差,找出这个最小平方误差最小的 feature,作为我们选择 feature 。
对于分类树,定义基尼系数 Gini index
Gini(p) = SUM_k( p_k *(1.0 - p_k)) = 1 - SUM_k(p_k^2)
p_k 表示样本点属于 k 类别的概率。
算法停止的条件是结点中样本数小于阈值,或者基尼指数小于阈值,或者没有更多的特征。
CART 剪枝
CART 算法也需要剪枝来防止过拟合。
重新定义 loss function
= C(T) + a * |T|
其中 |T| 定义为树的节点个数。
代码
徒手写了一个 decision tree,没有考虑剪枝,好累 code
另外再给一份 《机器学习实战》 提供的 决策树代码 decision tree -- machine learning in action
import numpy as np
class Tree():
def __init__(self):
'''
for leaf node,
label:
label value which is >=0
select_feature:
select_feature_val:
neg_tree, pos_tree:
useless, None
for non-leaf node,
label:
useless, -1
select_feature:
select feature index to make decision, >=0
select_feature_val:
select feature value to make decision, int value
neg_tree:
the Tree() boject to take a look for sample with select_feature value != select_feature_val
pos_tree:
the Tree() boject to take a look for sample with select_feature value == select_feature_val
'''
self.select_feature = None
self.select_feature_val = None
self.neg_tree = None
self.pos_tree = None
self.label = -1
class DecisionTreeClf():
def __init__(self):
self.tree = None
def calc_gini_index_val(Y):
labels, counts = np.unique(Y, return_counts = True)
total_counts = float(sum(counts))
probs = counts / total_counts
gini_index_val = 1.0 - sum(probs * probs)
return gini_index_val
def fit(self, X, Y):
def build_tree(X, Y, feature_list):
if Y.shape[0] == 0: # no samples
return None
if len(feature_list) == 0 or np.max(Y) == np.min(Y):
# no features, or there's only one label in the samples
tree = Tree()
labels, counts = np.unique(Y, return_counts = True)
tree.label = labels[np.argmax(counts)]
return tree
# print('X shape = ', X.shape)
# print('Y shape = ', Y.shape)
assert X.ndim == 2, 'input X should be an 2 D ndarray'
assert Y.ndim == 1, 'input Y should be an 1 D ndarray'
assert X.shape[0] == Y.shape[0], 'sample size not match for X/Y'
assert Y.dtype == np.int, 'Y datatype should be int'
assert X.dtype == np.int, 'X datatype should be int'
best_feature = -1
best_feature_val = None
best_gini_val = None
best_pos_sample_idx_list = None
best_neg_sample_idx_list = None
for select_feature in feature_list:
X_select = X[:, select_feature]
select_feature_val_list = np.unique(X_select)
if len(select_feature_val) == 1:
continue
for select_feature_val in select_feature_val_list:
pos_sample_idx_list = X_select == select_feature_val
neg_sample_idx_list = X_select != select_feature_val
pos_Y = Y[pos_sample_idx_list]
neg_Y = Y[neg_sample_idx_list]
pos_gini = calc_gini_val(pos_Y)
neg_gini = calc_gini_val(neg_Y)
pos_gini = float(pos_Y.shape[0] / Y.shape[0]) * pos_gini
neg_gini = float(neg_Y.shape[0] / Y.shape[0]) * neg_gini
feature_val_gini = pos_gini + neg_gini
if best_feature == -1 or feature_val_gini < best_gini_val:
best_feature = select_feature_val
best_feature_val = select_feature
best_gini_val = feature_val_gini
best_pos_sample_idx_list = pos_sample_idx_list
best_neg_sample_idx_list = neg_sample_idx_list
tree = Tree()
tree.select_feature = best_feature
tree.select_feature_val = best_feature_val
tree.neg_tree = Tree()
tree.pos_tree = Tree()
remain_feature_list = copy.copy(feature_list)
remain_feature_list.remove(select_feature)
tree.pos_tree = build_tree(X[best_pos_sample_idx_list, :], Y[best_pos_sample_idx_list], tree.neg_tree, remain_feature_list)
tree.neg_tree = build_tree(X[best_neg_sample_idx_list, :], Y[best_neg_sample_idx_list], tree.pos_tree, remain_feature_list)
return tree
feature_list = list(range(X.shape[1]))
self.tree = build_tree(X, Y, feature_list)
self.feature_size = X.shape[1]
def predict(self, X):
assert X.shape[1] == self.feature_size
tree = self.tree
Y = np.zeros((X.shape[0], ), np.int) - 1
for sample_idx in range(X.shape[0]):
tree = self.tree
while tree:
if tree.label != None or tree.label == -1:
Y[sample_idx] = tree.label
break
if X[sample_idx, tree.select_feature] == tree.select_feature_val:
tree = tree.pos_tree
else:
tree = tree.neg_tree
return Y